Snakes and Ladders is a popular game that we all played as children. For those of you who are new to the game, it’s a simple game played on a board that consists of 10×10 squares. The player moves by throwing a dice, you start from square 1, and move your way up to square 100. Some squares have ‘ladders’ that can propel you forward a few moves, and other squares have ‘snakes’ that would send you back a few moves. The goal of the game is to reach square 100 first. You can find more info on the game mechanics on the wiki.
I’ll show you here how to create a simple algorithm to solve the game. We will find out how many throws of the dice is necessary to win the game.
Breadth First Search Directed Graph
There are many graphing algorithms available, but the most appropriate one for us is Breath First Search. This algorithm is used to find the shortest path between two vertices on the graph. Every vertex starts with a root vertex, and every vertex on the graph has an adjacency list. Which is basically a list of vertices that can be reached from that node. Vertices are connected by edges. So to find the shortest path between two vertices you only need to count the number of edges between them.
In our case vertices are squares on the board, and edges are dice throws. Since a dice we’re using has 6 possible values, every square can be connected to 6 other squares (obviously the last 6 squares will be connected to less than 6 other squares).

Let’s go through a simple example, and follow a ‘happy path’. Examine the graph below:
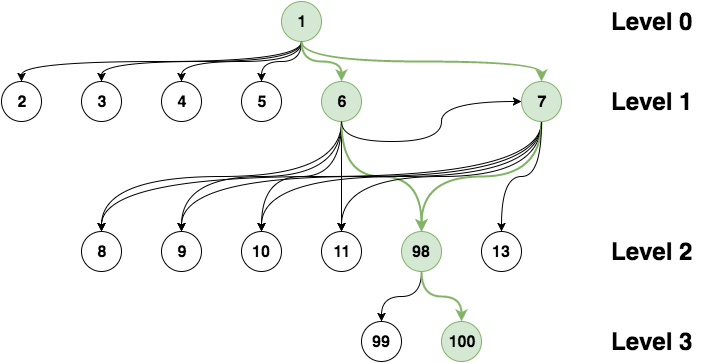
On the board we have a ladder that leads from square 12 to square 98. Which in effect means, every time you land on square 12, you’ll be on square 98 (so, basically, there is not square 12). If we start from square 1, roll the dice and land of the square 6 (or 7), we roll the dice again and end up on the square 12 (which propels us forward to square 98), then we roll the dice again, and finish the game on the square 100. From here, it’s obvious that we need three dice rolls to finish the game.
The graph above is split in levels, the levels are valid for a happy path that’s displayed in green above. And each level represents a dice throw. So, obviously, to get the minimum number of dice throws, we just need to get the minimum level of the vertex 100, and that’s pretty much it 🙂
Solution
Let’s try to work this out in swift.
So, we’ll need a basic class, let’s call it ‘Graph’. It will hold it’s vertex number (the number of the square), and it will have a list of the squares reachable from this square (the adjacency list), and we’ll add the minimum level of the vertex (just to make things easier for us).
class Graph {
var V: Int
var adj: [Graph] = []
var level: Int?
init(vertex: Int) {
self.V = vertex
}
}
We will have to iterate through all the squares on our board and create the adjacency list for each square. We can do this easily with this function:
func createEdges(vertexes: [Int: Graph], board: [Int: Int]) {
guard V < 100 else { return }
for i in 1...min(100 - self.V, 6) {
if let edge = board[V + i], let child = vertexes[edge] {
addEdge(w: child)
}
}
}
After we have created the entire graph, all we have to do is calculate the minimum level for each square with this function:
func setLevels(parent: Int = -1) {
level = parent + 1
for vertex in adj {
if let vertexLevel = vertex.level, vertexLevel > level! + 1 {
vertex.setLevels(parent: level!)
} else if vertex.level == nil {
vertex.setLevels(parent: level!)
}
}
}
And that’s pretty much it, we print the level of the last square, and we’ll get our minimum number of dice throws.
Final words
I ran across this problem on HackerRank.com, and it was a very interesting one for me. As an iOS developer I didn’t really ran across a problem like this in my career, so this was very exciting for me. I hope this helped you a bit, and I hope you had a lot of fun solving the challenge 🙂 You can find my playground on my github account.

👏👏👏
Thank you for the post. Quite useful