In computer science there are many data structures. In this post we will examine one such structure called a ‘Stack’. We’ll implement it using another data structure called a ‘Linked List’, and for the sake of comparison, we will implement the same stack data structure using plain old arrays, and compare performances between the two.
Stack
Stack is a LIFO data structure (Last In First Out). Which basically means, the last element that you add to the stack is the first one that you’ll pull out. I good analogy would be your email inbox. The most recent mail will be shown at the top, and if you read your mails from top to bottom, you’ll read your most recent mails first. If you’re getting hundreds of mails a day, this might mean you’ll never see some of the mails that are on the bottom of your stack.
Some common operations on a stack are push, pop and peek. Push will, obviously, push an item onto a stack. Pop will return the item, and delete it from the stack, and peek will allow you to see what the item at the top of the stack is, but it will not remove it..
Let’s say you have five items on your stack like the image below shows:
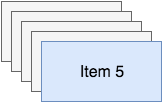
You can push an item onto your stack, let’ say you want to push item six on it:
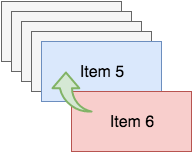
Now you have six items on the stack, and item five is no longer available to you, like so:
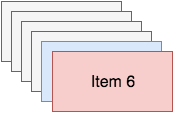
Now you can push another item on the stack, or you can pop an item from the stack. If you call the pop operation, you’ll get back item six, and that item will be removed from the stack, like the following image illustrates:
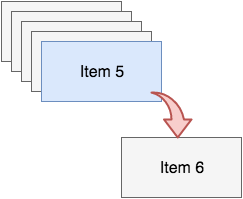
Now we’re back where we started, with five items on the stack.
Linked List
A linked list is a data structure used to represent a collection of elements in a form of, well, a list 🙂 What makes a linked list special is that every element has a pointer to the next element in the list, and if that pointer is nil, then you know you’ve reached the end of the list.
Every element in the list has a pointer to the next element, and the list itself has a pointer to the first element of the list, called a ‘Head’:

If you add a new element to the beginning of the list, all you have to do is change two pointers, the ‘Head’ pointer, and point the new element to the old ‘Head’ pointer:

If you compare a linked list with your standard array, the main difference would be in fetching the elements. Arrays are index based, linked lists are pointer based. Which means, if you need to fetch an element from the middle of the collection, with arrays you could do it in a constant time, but with a linked list you would have to traverse the collection and search for your element, so the complexity for accessing a random element in the array would be O(n).
That certainly is a hindrance, if you need to access a random element, but for our stack we only need to know the first element, and this is where the linked list shines. In this case the complexity of adding a new element to the linked list is constant O(1), but for the array the complexity would be O(n). Because the array would have to shift all of the items in the array by one, and insert your new item at the beginning of the array.
Solution
Let’s get to the fun part, we’ll implement a stack in swift 3.0. Btw, you can find the example project on my github account.
As the title of this blog post says, we’ll be implementing a stack using a linked list, so to start it off, we’ll need a node class:
private class Node<T> {
var item: T
var next: Node?
init(withItem item: T) {
self.item = item
}
}
This is a private class that will be used only by our DAStack internally. It’s a simple one, it has only two properties, one to store the item that we’re adding to the stack, and another to store the pointer to the next element.
With our node in place, we’ll need the actual stack, so let’s examine the DAStack class:
public class DAStack<T> {
private var head: Node<T>?
private var count: Int = 0
public var isEmpty: Bool {
return head == nil
}
public var size: Int {
return count
}
public func push(item: T) {
let oldHead = head
head = Node(withItem: item)
head?.next = oldHead
count += 1
}
public func pop() -> T? {
let item = head?.item
head = head?.next
count -= 1
return item
}
public func peek() -> T? {
return head?.item
}
}
As we can see, at the top of the class we have a pointer to the head of our linked list, we have some utility methods to fetch the count of the elements, and to check if the list is empty or not, and the important methods, push and pop. If we examine the push method in more detail we can see that we’re just creating a new node with the item we’re pushing, and setting the new items’ next pointer to the old head, and, of course, updating the current head to point to the new item. The pop function works pretty much in reverse of what we just described.
That’s pretty much it for the stack with a linked list. But let’s examine an alternative implementation using an array as a backing store, instead of a linked list.
Stack With an Array
Linked list implementation might seem a bit complex, and you might be thinking: “Why not use an array to do the same thing”. After all, it’s a lot simpler. So let’s do it:
public class DAArrayStack<T> {
private var items: [T] = []
public var isEmpty: Bool {
return items.isEmpty
}
public var size: Int {
return items.count
}
public func push(item: T) {
items.insert(item, at: 0)
}
public func pop() -> T? {
return items.count > 0 ? items.removeFirst() : nil
}
public func peek() -> T? {
return items.first
}
}
This is it, the whole implementation. It’s a lot simpler than the linked list, and it has the same interface. So there must be a catch. The performance is the catch, and we’ll examine it in the next section where we’ll compare the two implementations.
Linked List vs. Array Implementation
At first glance the two implementations are pretty much the same, but the linked list implementation seems a bit more complicated. So why should we use the linked list implementation, instead of the array implementation. One simple reason, performance. The performance difference in these two implementations is simply staggering.
Let’s examine the complexity of the push operation. Using the array, the complexity of the push is O(n), which means, that for every push operation the algorithm needs to shift all the items in the array in order to add the new element to the beginning of the array. But for the linked list implementation the complexity is O(1), which means that the complexity is constant. Every time we push an element, we’ll perform exactly the same number of operations, add element, and change two pointers, that’s it.
Let’s examine these differences in a table (values displayed are in seconds):
| 100k | 200k | 400k | 1M | |
|---|---|---|---|---|
| Linked List | 0,04 | 0,06 | 0,11 | 0,23 |
| Array | 2,85 | 13,38 | 199,4 | 1755,5 |
Astonishingly we can see that it would take about half an hour to process 1 million items using an array implementation, while it would take a fraction of a second using a linked list implementation. Here are the same values on a logarithmic graph:
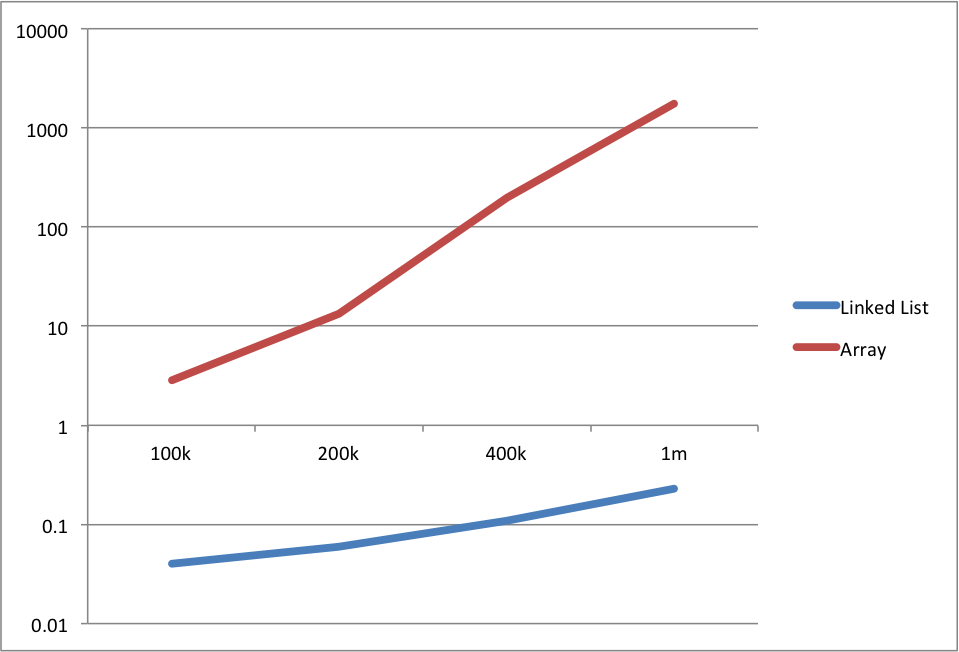
These are the values I see on my machine, the values on your machine might defer slightly, but the relative values should remain the same, linked lists implementation will be a lot faster, if you run the algorithm on your machine.
Conclusion
If you’re trying to process a small amount of data, it won’t really matter what algorithm you use (some say that if you’re trying to process less then 500 items, it doesn’t matter what algorithm you use). But if you’re trying to process a large amount or data, choosing a correct algorithm might be the difference between a working program and a non working one.
I hope this blog post gave you a taste of algorithms, and it’s importance in computer science. And I hope you’ll find it a bit useful in your daily life.
As always, have a nice day, Dejan 🙂

Pingback: Data structures and algorithms – Data structures and algorithms
Pingback: Queue With Doubly Linked List in Swift | agostini.tech
Pingback: Big O Notation | agostini.tech