Sorting algorithms are an important feature of modern computing, and in this article we’ll examine some of the most common sorting algorithms in use today. Implementations of these algorithms will be done in swift, but they are language agnostic, and you should have on problems implementing them in a language of your choice.
Most modern languages already offer an efficient sort implementation (this is also true with swift), so we can look at this article as a basis for academic discussion on sorting algorithms.
Selection Sort
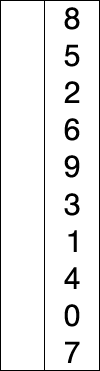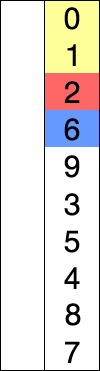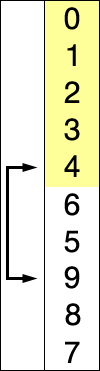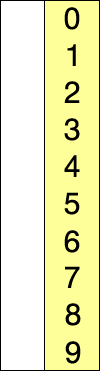
First on our list of sorting algorithms is Selection Sort. Selection sort algorithm set the current minimum item (item[0]) and will iterate over an array of items. It will search for the smallest item, when it’s finished iterating over the array, it will replace the smallest item it found with the current minimum item. In the next iteration of the algorithm the current minimum item will be moved to the next item in the array (item[1]) and the search for the smallest item begins again.
Here is a graphical representation of the algorithm:
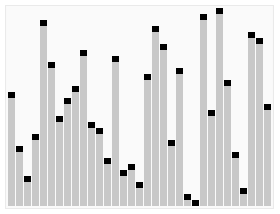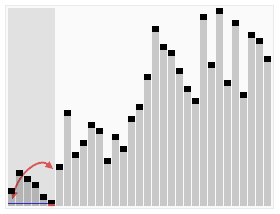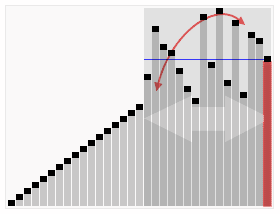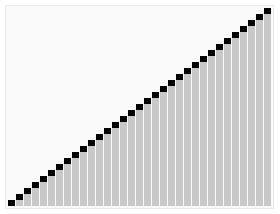
And here is the same algorithm displayed on a graph:
Implementing this algorithm is pretty straight forward, here is the swift implementation:
class DASelectionSort<T: Comparable> {
public static func sort(_ items: [T]) -> [T] {
var result = items
let length = result.count
for i in 0..<length {
var minIndex = i
for j in i+1..<length {
if result[j] < result[minIndex] {
minIndex = j
}
}
result.swapItems(itemAtIndex: i, withItemAtIndex: minIndex)
}
return result
}
}
From the algorithm we can see that the complexity of the algorithm is O(n2/2), so it’s quadratic (which is evident considering we have two for loops).
Before we start describing the other algorithms, let’s examine one utility function we used to make our algorithm implementations a bit more readable. It’s the swapItems array extension:
public mutating func swapItems(itemAtIndex firstIndex: Index, withItemAtIndex secondIndex: Index) {
if firstIndex != secondIndex {
swap(&self[firstIndex], &self[secondIndex])
}
}
As the name suggests, we’re using this method to swap items in the array. We’re manipulating pointers here directly, because it’s more efficient, that’s pretty much all the method is doing.
Insertion Sort
Insertion Sort is a sort algorithm that card players like to use to sort the cards they hold, and as selection sort, it’s pretty straight forward.
Using this algorithm you’re looking at the next element, and you’re trying to find a place for it by comparing it to the previous element, while the element you’re observing is smaller that the previous element, you’ll switch the two elements. Essentially sorting it into place.
Let’s see a graphical representation of the algorithm:
And a graph representation:
Swift implementation of the algorithm follows:
class DAInsertionSort<T: Comparable> {
public static func sort(_ items: [T]) -> [T] {
var result = items
let length = result.count
for i in 1..<length {
for j in stride(from: i, to: 0, by: -1) {
if result[j] < result[j - 1] {
result.swapItems(itemAtIndex: j, withItemAtIndex: j - 1)
} else {
break
}
}
}
return result
}
}
The complexity of this algorithm is O(N2/4) on average, which is a bit better than the Selection Sort.
Here is another implementation of the same algorithm using shifting instead of swapping:
public static func sortWithShifting(_ items: [T]) -> [T] {
var result = items
let length = result.count
for i in 1..<length {
var j = i
let temp = result[j]
while j > 0 && temp < result[j - 1] {
result[j] = result[j - 1]
j -= 1
}
result[j] = temp
}
return result
}
The algorithm is the same, but the implementation is a bit different. We remember the next unsorted item ‘temp’ and shift all the other sorted items to the right by one, and when we find a position for the temp item, we just insert it into position.
As it turns out, swapping pointers in swift is not as cheap as you would expect, and the second algorithm is quite a bit faster than the first one.
Shellsort
Shellsort is similar to insertion sort in that it exchanges elements to sort. The difference is that insertion sort exchanges elements that are close together, while the shellsort exchanges elements that are far apart. We would compare every h-th element and sort them, this way we would get an array that is h-sorted. After h passes through the array we will have h sorted subarrays, then we decrease h and run the algorithm again, by the time h reaches 1 we will have a sorted array.
Here is a visual representation of the algorithm on a graph:
And the implementation of the algorithm in swift:
class DAShellSort<T:Comparable> {
public static func sort(_ items: [T]) -> [T] {
var result = items
let length = result.count
var h = 1
while h < length / 3 {
h = 3 * h + 1
}
while h >= 1 {
for i in h..<length {
for j in stride(from: i, to: h - 1, by: -h) {
if result[j] < result[j - h] {
result.swapItems(itemAtIndex: j, withItemAtIndex: j - h)
} else {
break
}
}
}
h /= 3
}
return result
}
}
Shellsort is much faster than insertion or selection sorts, and as the array grows in size the difference is speed is a lot more obvious. We can see from the implementation of the algorithm that it’s very similar to the insertion sort, we decrement the index by h instead of 1, and we reduce the h for the next iteration, and that’s pretty much it. We could say that shellsort is made up of many smaller insertion sorts.
Mergesort
Mergesort is one of the ‘divide and conquer’ sorting algorithms. It’s beautiful in its simplicity. You split your array into two subarrays, you sort the subarrays and merge the to subarrays into one. The trick is to recursively split the array until your subarray has one or two elements, then the sort operation is just a simple comparison. Once you sorted your smallest subarrays you just merge them all back up, and there you go, sorted.
Here’s an animation of the algorithm:
And a visualisation of the algorithm on a graph:
And finally some swift code:
class DAMergeSort<T: Comparable> {
public static func sort(_ items: [T]) -> [T] {
var result = items
var temp = result
sort(original: &result, temp: &temp, low: 0, high: result.count - 1)
return result
}
private static func sort(original: inout [T], temp: inout [T], low: Int, high: Int) {
if high <= low { return }
let mid = low + (high - low) / 2
sort(original: &original, temp: &temp, low: low, high: mid)
sort(original: &original, temp: &temp, low: mid + 1, high: high)
merge(original: &original , temp: &temp, low: low, medium: mid, high: high)
}
private static func merge(original: inout [T], temp: inout [T], low: Int, medium: Int, high: Int) {
var i = low
var j = medium + 1
for k in low...high {
temp[k] = original[k]
}
for k in low...high {
if i > medium {
original[k] = temp[j]
j += 1
}
else if j > high {
original[k] = temp[i]
i += 1
}
else if temp[j] < temp[i] {
original[k] = temp[j]
j += 1
}
else {
original[k] = temp[i]
i += 1
}
}
}
}
From the code we can see that we’re recursively calling the sort method until we hit the escape condition (when low and high meet), this leaves us with a subarray of size 2, when we hit the merge call for the first time in the deepest recursion. From here on it’s a simple compare and copy in the merge function.
Performance of the merge sort is a bit better than shellsort for smaller arrays, but when we move to larger arrays the performance benefits are more evident, as we’ll see later.
Quicksort
Last but not the least on our list is the Quicksort. Quicksort is arguably the best sorting algorithm today, it’s most analysed, most tested, and most implemented. It’s also a ‘divide and conquer’ type of an algorithm like mergesort.
Using quicksort you would select an item from the array, and compare it with other elements, you would place smaller elements to the left, and larger to the right, when you’re finished with the first iteration, you will have the observed item in its final position, then you just repeat the same steps for the resulting two subarrays.
Here’s a visualisation of the algorithm:
And the code:
class DAQuickSort<T: Comparable> {
public static func sort(_ items: [T]) -> [T] {
var result = items
result.shuffle()
sort(original: &result, low: 0, high: result.count - 1)
return result
}
private static func sort(original: inout [T], low: Int, high: Int) {
if high <= low { return }
let j = partition(original: &original , low: low, high: high)
sort(original: &original, low: low, high: j - 1)
sort(original: &original, low: j + 1, high: high)
}
private static func partition(original: inout [T], low: Int, high: Int) -> Int {
var i = low
var j = high + 1
let v = original[low]
while true {
i += 1
while original[i] < v {
i += 1
if i == high {
break
}
}
j -= 1
while v < original[j] {
j -= 1
if j == low {
break
}
}
if i >= j {
break
}
original.swapItems(itemAtIndex: i, withItemAtIndex: j)
}
original.swapItems(itemAtIndex: low, withItemAtIndex: j)
return j
}
}
Performance of the quicksort is by far the best of the algorithms described here, the only problem with quicksort is that it’s dependant on the input. If your input array is sorted, then the algorithm will perform badly, that’s why we shuffle the array before we perform the sort.
Performance Comparison
I wrote some unit tests to measure the performance of these algorithms, and just for the fun of it, I also measure the performance of the swifts Array built in sort.
Here’s the graph (values on the Y-Axis are seconds):
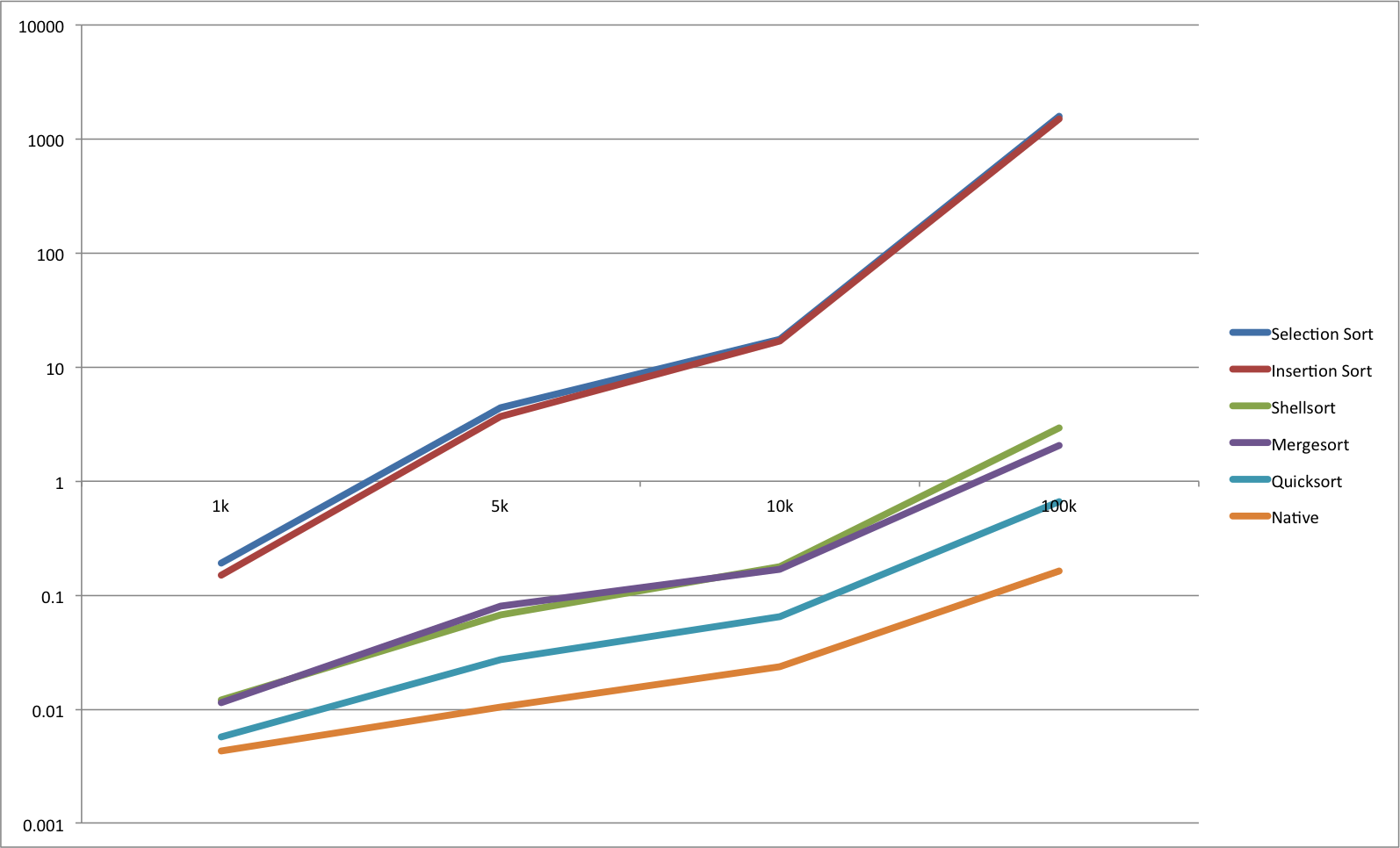
And the values in the table (values are also in seconds):
| 1k | 5k | 10k | 100k | |
|---|---|---|---|---|
| Selection Sort | 0,19 | 4,39 | 17,70 | 1575,63 |
| Insertion Sort | 0,15 | 3,71 | 16,89 | 1498,61 |
| Shellsort | 0,012 | 0,067 | 0,18 | 2,95 |
| Mergesort | 0,01 | 0,08 | 0,17 | 2,07 |
| Quicksort | 0,006 | 0,03 | 0,065 | 0,67 |
| Array Sort | 0,004 | 0,01 | 0,02 | 0,16 |
The scale of the Y-Axis is logarithmic. From the graph it’s evident that some sorting algorithms are better than others 🙂 Selection and insertion sort are neck and neck in performance, and are the worst performing algorithms. They’re OK for smaller arrays, but once the number of array items is measured in thousands, some other algorithm might be a better choice. Processing a million items using these algorithms could easily take a few hours. Which is unacceptable for some applications. Next up are shellsort and mergesort, which are not that bad, 100k items in a few seconds, is pretty good, but the quicksort is a clear winner here. It sorts the array in under a second, which is amazing. I ran the comparison with the native array sort (orange line on the graph), to be honest, I expected the native implementation to outperform my quicksort implementation, but it’s over three times faster, which is amazing. We all know that the native implementation is using quicksort for large arrays, but the guys must be using an optimised quicksort with 3-way partitioning (maybe a topic for one of the next posts 🙂 )
Conclusion
And there you have it. We saw five different sorting algorithms being implemented, and saw that it’s important which algorithm you choose for the job. Selecting a wrong algorithm might be a difference between a working app and a non working one. We also learned from this post that the swift array sort implementation is far better than these implementations we’re seeing, so we might just as well use that 😀
This post was more of an academic discussion, and I hope you enjoyed reading it. You can find all the coding examples from this article on my GitHub account.
Have a nice day 🙂
Dejan


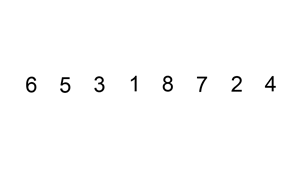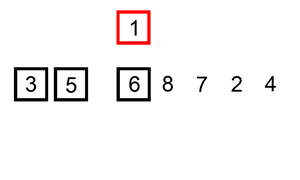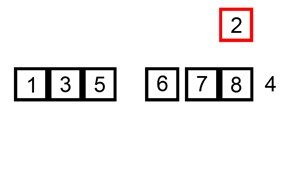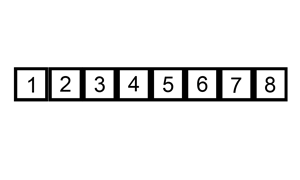
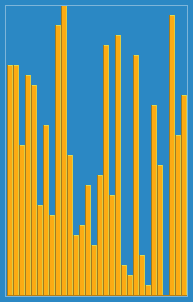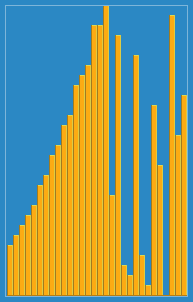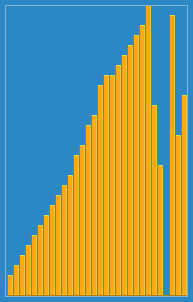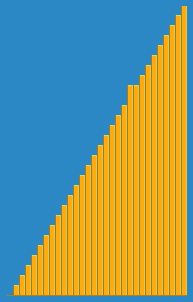

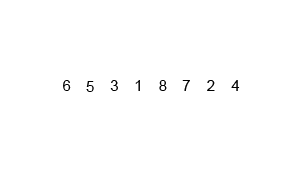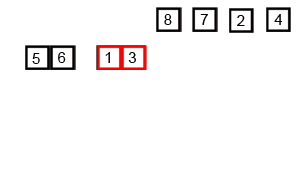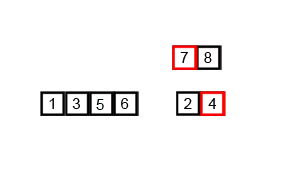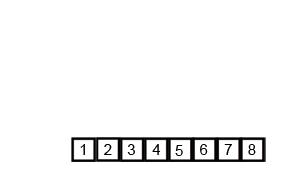

Very Useful