 Bellman-Ford algorithm is a very versatile algorithm for finding the shortest path on an edge weighted directed graph. It differs from Dijkstra’s algorithm in that it can handle the negative cycles on the graph. In this article we’ll implement the Bellman-Ford algorithm in swift and with it conclude our journey with directed graphs… for now 🙂
Bellman-Ford algorithm is a very versatile algorithm for finding the shortest path on an edge weighted directed graph. It differs from Dijkstra’s algorithm in that it can handle the negative cycles on the graph. In this article we’ll implement the Bellman-Ford algorithm in swift and with it conclude our journey with directed graphs… for now 🙂
Bellman-Ford Algorithm
We already covered Dijkstra’s algorithm but, just to remind you… In Dijkstra’s algorithm we used a priority queue to relax the vertices. We would relax the edges of a vertex only if we found that the destination vertex has a shorter path to a destination than the existing shortest path. You can read more about it in this article.
Bellman-Ford is actually simpler than Dijkstra’s algorithm. It’s using a simple FIFO queue. Bellman-Ford algorithm will also check if the next destination is shorter that the current shortest path, just like Dijkstra’s algorithm. If it is, it will simply add that destination vertex into a queue if it’s not already in the queue. We talked about how to implement a FIFO queue, you can read all about it in this article. We’ll be using this implementation for our implementation of Bellman-Ford.
Dijkstra’s algorithm is faster than Bellman-Ford, but Bellman-Ford algorithm can detect negative cycles on the graph. This makes Bellman-Ford a lot more flexible. If you know that your graph can’t have negative cycles, you’re better off using Dijkstra’s algorithm. If you’re not sure, than you should use Bellman-Ford. We had a whole article on how to detect cycles on a directed graph, check it out. In our implementation of Bellman-Ford we’ll be using the cycle detector that we created for that article.
The Example
Your vertices and edges can represent anything you want. In our example we’ll imagine we have a network of computers spread across the world. The city names will be our vertices. The links between the computers will be our edges. Some links will be bi-directional some will be uni-directional. Our example will look like this:
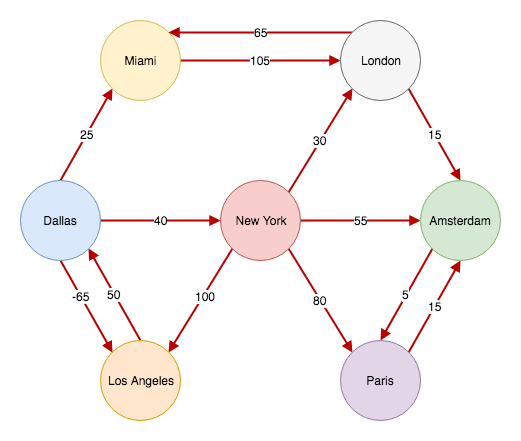
New York will be our source. We want to know the shortest (or the cheapest in our example) routes to the other servers.
Ideally, we would have a shortest path like this one (we’re ignoring the link from Dallas to Los Angeles here):
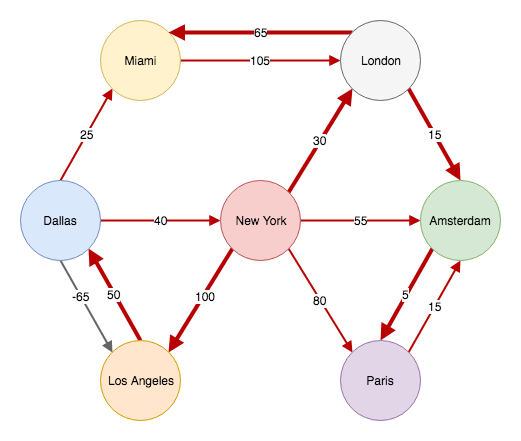
But this graph has a negative edge that’s going from Dallas to Los Angeles. When we start relaxing our edges, we’ll eventually relax all the edges that have Dallas as a source. One of them will be the negative edge that points to Los Angeles. Keep in mind that from the point of New York, the cost to reach Los Angeles is ‘100’. And the previous edge on our shortest path to Los Angeles is actually New York. When we relax the negative edge, the cost to Los Angeles will change to ’85’, because of the negative weight. And the previous edge on the shortest path will be changed to Dallas. This is a problem, because it creates a cycle:
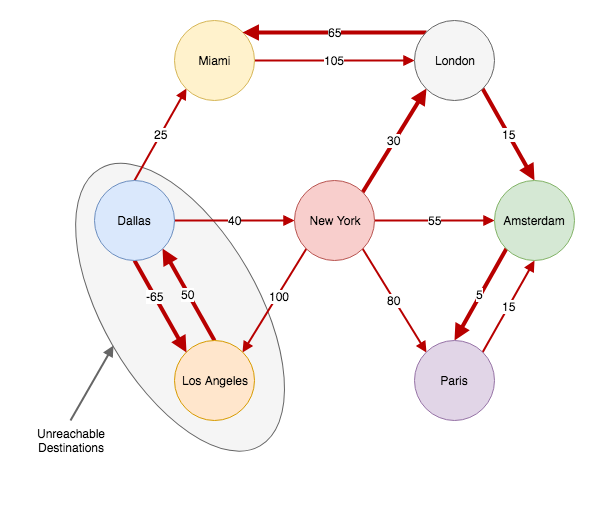
Originally, Dallas was only reachable through Los Angeles. And now, Los Angeles thinks its shortest path should lead through Dallas. If we try to reconstruct our shortest path these two destinations will point to each other, and we’ll end up in a loop.
Even worse, because of the negative weight the cost to the destination will constantly decrease, and the algorithm will be stuck in an infinite loop trying to relax the edges between Dallas and Los Angeles. For this reason it’s really important to periodically check for negative cycles and stop the algorithm from running.
Now it’s time to see some code…
Implementation
For our implementation of Bellman-Ford algorithm we’ll use the ATQueue class that we implemented in one of the previous articles. We’ll also need a way to detect cycles on a graph. We covered this topic as well and we’ll use a class we’ve created in that article. Some of the functions will be virtually identical to the functions we’ve already covered in our article on Dijkstra’s algorithm, so we’ll skip them here.
These are the variables our implementation will be using:
Some of them should look familiar from the implementation of the Dijkstra’s algorithm. The ones to take note of are the ‘relaxationQueue’ and the ‘iteration’. The ‘relaxationQueue’ is a queue of vertices that are queued for relaxation. We’ll use the ‘iteration’ counter to periodically check for negative cycles on the graph.
We’ll start our algorithm right from the initialiser:
We initialise all our destinations and set the total weight for our source to ‘0’. We add our source vertex to the ‘relaxationQueue’ and start the algorithm. We’ll break out of this loop if the ‘relaxationQueue’ is empty, or if we’ve detected a negative cycle.
The ‘relax’ function is quite simple:
If the path to a destination vertex is shorter than the existing shortest path, we add the destination vertex to the ‘relaxationQueue’ if it’s not in the queue already. At the end of the function we increase our iteration counter and periodically check for negative cycles. You could check for negative cycles after your iteration count reaches the number of vertices, or after it reaches the number of edges, it’s up to you. As long as you periodically check for negative edges.
Negative Cycles
Detecting negative cycles is going to be the heart of the algorithm. We already discussed how to detect cycles in a digraph. We’ll be using the class we implemented in that article to detect cycles. Our cycle detector class takes in a graph as the initialiser argument. We can’t just pass in our current graph as the argument. We want to know if our shortest path has a cycle. Take a look at our shortest path graph once again:

We want to create a new graph that contains only the currently relaxed vertices with the shortest path. In other words, we only want to pass in the thick red edges from the graph above, along with the vertices they’re connected to.
If we detect a cycle on this graph, then by definition we’ll have a negative cycle. Because the only situation in which we can have a cycle on a shortest path tree is if an edge has a negative value and it’s part of a cycle.
Now, if you look at our function for detecting cycles it should be clear to you what we’re trying to do here:
If the destination is reachable in our current graph we add the destination, its previous vertex and the connecting edge to the new graph. Once we do this for all the destinations all we do is create an instance of our cycle finder class and check if it has a cycle. If we detect a cycle we assign it to our ‘negativeCycle’ property of the class.
Testing It Out
Let’s see how our example works in practice… First we create our vertices, our edges and add them to the graph:
After which we create our instance of the Bellman-Ford class with the graph we just created and with ‘New York’ as the source vertex:
When we run our test code we’ll see an output like this one:
We can clearly see the cycle in this graph printed out.
Conclusion
In this article we’ve used the knowledge from the previous two articles on queues and detecting cycles to implement the Bellman-Ford algorithm. Bellman-Ford is a bit slower than Dijkstra’s algorithm, but it’s more flexible, because it can handle a graph that has negative cycles. If you’re not sure if your graph will have negative cycles or not, you’re better off using the Bellman-Ford algorithm.
This has been a short and fun article on detecting a shortest path on graphs that might have negative cycles. We’ll take a little break from graphs for now and move on to something different 🙂 You can find all the code in the GitLab repo along with all the code snippets from this article.
I hope you’ve enjoyed this article and that you’ve learned something new today. And, as usual, have a nice day 🙂
~D;

Great article Dejan, as always.
Thanks Jasper 🙂